Keep Talking & Nobody Explodes là một trò chơi gỡ bom ưa thích của lamter. Cậu ấy có thể dễ dàng giải rất nhiều module trong thời gian nhanh chóng. Tuy nhiên, module dưới đây là điều mà lamter luôn gặp khó khăn.

Bạn được lamter cung cấp cho 1 số thông tin về quả bom. Nhiệm vụ của bạn là cho anh ấy biết cách gỡ quả bom này.

~\texttt{Input}~

• Dòng đầu tiên là serial của quả bom.
• Dòng thứ hai là số strikes hiện tại của bạn.
• Dòng cuối cùng lần lượt chứa thứ tự của đèn flash.

~\texttt{Output}~

• Một dòng duy nhất chứa kết quả của bài toán.

~\texttt{Sample Input}~

#dx3mbowqs
1
Red Red Green Blue

~\texttt{Sample Output}~

Yellow Yellow Blue Green

Quán cafe X là nơi tuyệt vời cho làm việc và học tập. TaThanHungbc là một vị khách thân thuộc của quán cafe này. Điều mà TaThanHungbc thích ở quán cafe này là ngoài những thức uống ngon, độc lạ mà nhà vệ sinh của quán cafe có rất nhiều tính năng hữu ích.

Một ngày nọ, khi TaThanHungbc đang chill ở quán cafe thì bỗng nhiên gặp một vụ ăn trộm vặt ở đây. Bằng suy luận của mình, TaThanHungbc đã mau chóng nhận ra rằng thứ tự vào nhà vệ sinh trong sự việc này là rất quan trọng. TaThanHungbc bắt đầu tra hỏi những khách hàng ở đây. Tuy nhiên họ chỉ biết người vào trước và người vào sau mình. Qua đó TaThanHungbc có thể dễ dàng đoán ra được ngay thứ tự vào nhà vệ sinh và giải quyết vụ việc.

Tuy nhiên lượng khách sử dụng nhà vệ sinh ở đây quá đông nên bạn hãy giúp TaThanHungbc tìm ra thứ tự vào nhà vệ sinh ở đây. Cho biết đối với người đầu tiên thì người đứng trước sẽ được giả sử là 0 và đối với người cuối cùng thì người đứng sau sẽ được giả sử là 0.

~\texttt{Input}~

• Dòng đầu tiên chứa số nguyên dương ~N~ , là số lượng khách hàng sử dụng nhà vệ sinh.

• Dòng thứ i trong số ~N~ dòng sau, chứa 2 số nguyên ~X~,~Y~ lần lượt là khách hàng vào trước và vào sau khách hàng ~i~.

~\texttt{Output}~

• Gồm ~N~ số là thứ tự sử dụng nhà vệ sinh của khách hàng ở đây

~\texttt{Constraint}~

• ~N \leq 5 * 10^5~.

~\texttt{Subtask}~

• Subtask ~1~ (~50\%~ số điểm): ~N \leq 10~.
• Subtask ~2~ (~50\%~ số điểm): Không có giới hạn gì thêm.

~\texttt{Sample Input}~

5
3 2
5 0
2 4
0 1
1 5

~\texttt{Sample Output}~

3 1 2 5 4

CodeTN có ~N~ thanh gỗ, thanh gỗ thứ ~i~ có độ dài là ~a_i~. Anh ấy quyết định dùng số gỗ này để xây hàng rào cho ngôi nhà.

Để xây hàng rào ngôi nhà của cậu ấy, chúng ta phải cần ít nhất ~K~ thanh gỗ độ dài bằng nhau. Vì vậy, các thanh gỗ có thể được cắt ra thành nhiều thanh gỗ độ dài nhỏ hơn.

Vì muốn an ninh của ngôi nhà được đảm bảo CodeTN muốn rằng những thanh gỗ này phải: "Càng cao càng tốt". Bạn hãy giúp CodeTN tìm ra độ dài lớn nhất có thể của những thanh gỗ này nhé.

~\texttt{Input}~

• Dòng đầu tiên chứa hai số nguyên dương ~N~, ~K~, lần lượt là số thanh gỗ mà CodeTN có và số thanh gỗ cần thiết để xây hàng rào cho nhà cậu ấy.

• Dòng thứ 2 chứa ~N~ số, thanh gỗ thứ ~i~ có độ dài là ~a_i~.

~\texttt{Output}~

• Một số duy nhất là kết quả của bài toán.
• Kết quả cần được in chính xác ~2~ số chữ số thập phân.

~\texttt{Constraint}~

• ~N \leq 10^6~.
• ~a_i~, ~K \leq 10^9~.

~\texttt{Subtask}~

• Subtask ~1~ (~20\%~ số điểm): ~n \leq 10~.
• Subtask ~2~ (~30\%~ số điểm): ~a_i \leq 1000~.
• Subtask ~3~ (~50\%~ số điểm): Không có giới hạn gì thêm.

~\texttt{Sample Input}~

3 4
2 3 8

~\texttt{Sample Output}~

2.66

vvngh có ~N~ tờ giấy kích thước khác nhau. Cậu ấy nghĩ ra một trò chơi thú vị. vvngh xếp những tờ giấy ở chân tường sát lại gần nhau theo thứ tự. vvngh quan sát và nhận thấy tờ giấy thứ ~i~ có chiều rộng ~w_i~ ô ly và chiều cao ~h_i~ ô ly. vvngh thắc mắc rằng liệu có bao nhiêu hình chữ nhật tạo được từ các ô ly của những tờ giấy khi xếp lại. Nhiệm vụ của bạn là giúp cậu ấy giải đáp thắc mắc này.

~\texttt{Input}~

• Dòng đầu tiên chứa số nguyên ~N~ là số lượng tờ giấy.
• ~N~ dòng tiếp theo mỗi dòng chứa hai số nguyên ~h_i~ và ~w_i~ biểu diễn chiều cao và chiều rộng của tờ giấy thứ ~i~

~\texttt{Output}~

• Gồm một số nguyên duy nhất là kết quả của bài toán.
• Vì kết quả có thể rất lớn nên hãy in ra phần dư khi chia cho ~10^9 + 7~.

~\texttt{Constraint}~

• ~1 \leq N \leq 10^5~
• ~1 \leq w_i~, ~h_i \leq 10^9~

~\texttt{Subtask}~

• Subtask ~1~ (~25\%~ số điểm): ~h_i = h_{i+1}~ với mọi ~i < N~.
• Subtask ~2~ (~25\%~ số điểm): ~h_i \leq h_{i+1}~ với mọi ~i < N~.
• Subtask ~3~ (~25\%~ số điểm): ~N \leq 1000~
• Subtask ~4~ (~25\%~ số điểm): Không có giới hạn gì thêm

~\texttt{Sample Input}~

3
3 1
2 1
1 1

~\texttt{Sample Output}~

15

~\texttt{Note}~

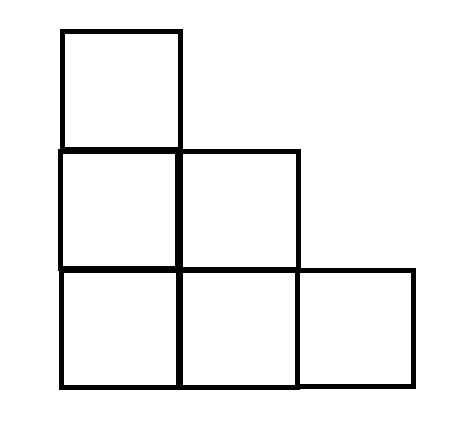
• Có ~6~ hình chữ nhật kích thước ~1\times1~.
• Có ~3~ hình chữ nhật kích thước ~2\times1~.
• Có ~3~ hình chữ nhật kích thước ~1\times2~.
• Có ~1~ hình chữ nhật kích thước ~2\times2~.
• Có ~1~ hình chữ nhật kích thước ~3\times1~.
• Có ~1~ hình chữ nhật kích thước ~1\times3~.

Vậy kết quả của ví dụ đầu tiên là ~6 + 3 + 3 + 1 + 1 + 1 = 15~

Trại hè QHHOJ được tổ chức với rất nhiều hoạt động và trò chơi kỳ thú. heygnauq đã vượt qua rất nhiều trò chơi thử thách và đến với giai đoạn cuối cùng là phần thưởng. Có ~N~ thẻ bài được xếp lần lượt thành một hàng. Thẻ bài thứ ~i~ có giá trị phần thưởng là ~a_i~. heygnauq buộc phải chọn ~3~ dãy thẻ bài liên tiếp bất kì. heygnauq không biết lựa chọn như thế nào để được thật nhiều phần thưởng. Bạn hãy giúp heygnauq thực hiện việc này.

~\texttt{Input}~

• Dòng đầu tiên chứa một số nguyên ~N~ là số thẻ bài.
• Dòng thứ hai chứa ~N~ số nguyên là giá trị phần thưởng thẻ bài thứ ~i~.

~\texttt{Output}~

• Gồm một số nguyên duy nhất là kết quả của bài toán

~\texttt{Constraint}~

• ~3 \leq n \leq 10^6~.
• ~|a_i| \leq 10^9~.

~\texttt{Subtask}~

• Subtask ~1~ (~10\%~ số điểm): ~n \leq 10~.
• Subtask ~2~ (~20\%~ số điểm): ~n \leq 10^2~.
• Subtask ~3~ (~30\%~ số điểm): ~n \leq 10^3~.
• Subtask ~4~ (~40\%~ số điểm): Không có giới hạn gì thêm.

~\texttt{Sample Input}~

7
-1 3 -3 5 -2 7 -1

~\texttt{Sample Output}~

15