Trật tự giao thông

Xem dạng PDF
Gửi bài giải
Điểm: 800 (OI)
Giới hạn thời gian: 1.0s
Giới hạn bộ nhớ: 256M
Input: stdin
Output: stdout
Tác giả:
heygnauq
Dạng bài
Ngôn ngữ cho phép
Ada, Assembly, Awk, Brain****, C, C#, C++, COBOL, D, Dart, F#, Forth, Fortran, Go, Groovy, Haskell, Intercal, Java, JS, Kotlin, Lisp, Lua, ObjC, OCaml, Pascal, Perl, PHP, Pike, Prolog, PyPy, Python, Racket, Ruby, Rust, Scala, Scheme, Scratch, Sed, Swift, TCL, Turing, VB, Zig

Thành phố X có dạng lưới N×M. Mỗi ô của lưới là một khu vực.

CodeTN là một kẻ lang thang muốn đi qua thành phố này. CodeTN phải đi từ ô (1,0) đến ô (1,1) để đi vào, và (N,M) đến ô (N,M+1) để thoát khỏi thành phố.

Tuy nhiên hệ thống giao thông ở đây lại rất nghiêm ngặt. Khi muốn đi từ khu vực này sang khu vực khác, người tham gia giao thông chỉ được di chuyển theo hướng mà mình đang đi(kể cả khi đi vào hay đi ra khỏi thành phố). Có K trạm đổi hướng giúp người tham gia giao thông có thể đổi hướng hiện tại sang 4 hướng. Việc sử dụng trạm đổi hướng này sẽ tốn một lượng chi phí khá đáng kể.

Nhà lữ hành CodeTN rất muốn đi qua thành phố này lại còn muốn sử dụng một lượng ít trạm đổi hướng nhất. Bạn hãy giúp CodeTN tính toán việc chi tiêu này nhé!

Input

  • Dòng đầu tiên chứa hai số nguyên N, M là kích thước của thành phố.

  • Dòng thứ hai chứa số nguyên K là số lượng của trạm đổi hướng.

  • K dòng tiếp theo mỗi dòng chứa hai số nguyên X, Y là tọa độ của trạm đổi hướng (1≤X≤N, 1≤Y≤M).

Output

  • Gồm một số nguyên duy nhất là số lượng trạm chuyển hướng ít nhất mà CodeTN cần dùng để đi qua thành phố này hoặc là −1 nếu CodeTN không thể đi qua thành phố này.

Constraint

  • 2≤N,M≤109
  • 1≤K≤min(N×M,2×105)

Subtask

  • Subtask 1 (15% số điểm): N=2, M≤5×103.
  • Subtask 2 (15% số điểm): N×M ≤20 .
  • Subtask 3 (20% số điểm): N, M ≤103 .
  • Subtask 4 (30% số điểm): N, M ≤2×105 .
  • Subtask 5 (20% số điểm): Không có giới hạn gì thêm .

Sample Input

Copy
3 5
6
1 3
2 2
2 3
3 2
3 4
2 5

Sample Output

Copy
4

Notes

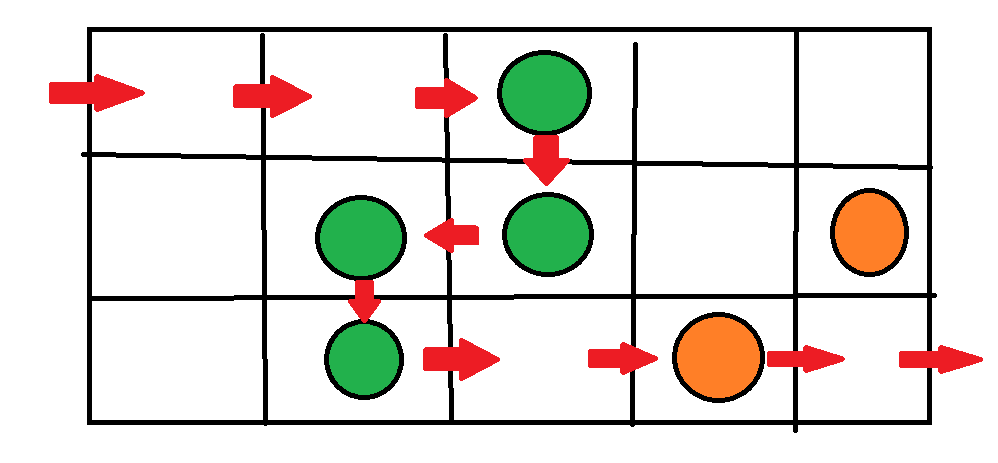
Bình luận

Hãy đọc nội quy trước khi bình luận.


  • 0
    vandung666      đã bình luận 3:30:28 ch, 13/02/2025

    include <bits/stdc++.h>

    using namespace std;

    struct Node { int r, c; bool canTurn; };

    struct Edge { int to;
    int dir;
    };

    int main(){ ios::syncwithstdio(false); cin.tie(nullptr);

    Copy
    int N, M; 
cin >> N >> M;
int K; 
cin >> K;
vector<Node> nodes;
nodes.push_back({1, 1, false}); 
for (int i = 0; i < K; i++){
    int x, y;
    cin >> x >> y;
    nodes.push_back({x, y, true});
}
nodes.push_back({N, M, false}); 
int totalNodes = nodes.size();  


unordered_map&lt;int, vector<pair<int,int>>> rowMap;
rowMap.reserve(totalNodes*2);
for (int i = 0; i < totalNodes; i++){
    int r = nodes[i].r, c = nodes[i].c;
    rowMap[r].push_back({c, i});
}

for(auto &p : rowMap){
    sort(p.second.begin(), p.second.end(), [](const pair<int,int> &a, const pair<int,int> &b){
        return a.first < b.first;
    });
}
unordered_map&lt;int, vector<pair<int,int>>> colMap;
colMap.reserve(totalNodes*2);
for (int i = 0; i < totalNodes; i++){
    if(nodes[i].canTurn){
        int r = nodes[i].r, c = nodes[i].c;
        colMap[c].push_back({r, i});
    }
}
for(auto &p: colMap){
    sort(p.second.begin(), p.second.end(), [](const pair<int,int> &a, const pair<int,int> &b){
        return a.first < b.first;
    });
}

vector<vector<Edge>> adj(totalNodes);

for(auto &p : rowMap){
    auto &vec = p.second;
    for (int i = 0; i + 1 < (int)vec.size(); i++){
        int u = vec[i].second, v = vec[i+1].second;
        adj[u].push_back({v, 0});
        adj[v].push_back({u, 1});
    }
}
for(auto &p : colMap){
    auto &vec = p.second;
    for (int i = 0; i + 1 < (int)vec.size(); i++){
        int u = vec[i].second, v = vec[i+1].second;

        adj[u].push_back({v, 2});

        adj[v].push_back({u, 3});
    }
}

const int DIRS = 4, INF = 1e9;
vector<vector<int>> dist(totalNodes, vector<int>(DIRS, INF));
deque<pair<int,int>> dq;

dist[0][0] = 0;
dq.push_back({0, 0});

while(!dq.empty()){
    auto [u, d] = dq.front();
    dq.pop_front();
    int cost = dist[u][d];
    if(u == totalNodes - 1 && d == 0){
        cout << cost << "\n";
        return 0;
    }
    for(auto &edge : adj[u]){
        if(edge.dir == d){ 
            int v = edge.to;
            if(dist[v][d] > cost){
                dist[v][d] = cost;
                dq.push_front({v, d});
            }
        }
    }


    if(nodes[u].canTurn){
        for (int nd = 0; nd < DIRS; nd++){
            if(nd == d) continue;
            if(dist[u][nd] > cost + 1){
                dist[u][nd] = cost + 1;
                dq.push_back({u, nd});
            }
        }
    }
}

cout << -1 << "\n";
return 0;

    } t mat ca thanh xuan ms full duoc qua kho