Khoa và Ngân là hai học sinh tài năng và đầy năng lượng. Hàng ngày, họ đọ tài trong mọi lĩnh vực, từ các bài kiểm tra đến các hoạt động ngoại khóa. Khoa luôn nỗ lực vượt qua Ngân, còn Ngân luôn tìm cách phản công và chống trả.

Một ngày nọ, họ quyết định tham gia một trò chơi mới - một trò chơi tưởng tượng, một trò chơi mà tất cả đều phải thể hiện sự sáng tạo và trí óc của mình.

Trò chơi sẽ bao gồm ~T~ ván, mỗi ván cả hai bạn sẽ được cho một hình gồm ~N~ điểm được đánh số từ ~1~ đến ~N~ và ~M~ đoạn nối giữa ~2~ điểm bất kỳ. Mỗi ván sẽ gồm nhiều lượt, bạn Khoa sẽ đi lượt đầu tiên, ở mỗi lượt thì người chơi của lượt đó cần phải chọn ra một điểm có số lượng đoạn thẳng nối với nó là chẵn và xóa đi điểm đó cùng các đoạn có một trong hai đầu mút là điểm đó. Đến lượt của ai mà người đó không thực hiện được hành động trên thì người đó sẽ thua.

Bạn hãy cho biết ở mỗi ván thì ai sẽ là người chiến thắng, biết rằng cả hai bạn đều là những người có lập luận logic, chiến thuật hoàn hảo và sẽ đưa ra cách chơi tối ưu nhất ở mọi tình huống.

Input

• Dòng đầu tiên chứa số nguyên dương ~T~ là số ván mà hai bạn sẽ chơi với nhau.

Trong mỗi ván:

• Dòng đầu tiên chứa hai số nguyên không âm ~N, M~ tương ứng là số lượng điểm và đoạn của hình.
• ~M~ dòng tiếp theo, dòng thứ ~i~ chứa hai số nguyên ~u, v~ (~1 \leq u, v \leq N~) thể hiện rằng đoạn thẳng thứ ~i~ nối giữa điểm thứ ~u~ và điểm thứ ~v~.

Output

• Gồm ~T~ dòng chứa kết quả của ~T~ ván đấu.

Với mỗi ván đấu:

• Nếu Khoa thắng thì bạn cần ghi ra “Khoa” (không có dấu ngoặc kép).
• Nếu Ngân thắng thì bạn cần ghi ra “Ngan” (không có dấu ngoặc kép).

Constraint

• ~1 \leq T \leq 10~.
• ~1 \leq N, M \leq 10^5~.

Subtask

• Subtask ~1~ (~15\%~ số điểm): ~N \leq 10~.
• Subtask ~2~ (~15\%~ số điểm): ~M = N - 1~ và từ một điểm bất kỳ có thể đi tới mọi điểm khác thông qua các đoạn thẳng.
• Subtask ~3~ (~15\%~ số điểm): Các điểm và đoạn thẳng không tạo thành chu trình.
• Subtask ~4~ (~55\%~ số điểm): không có giới hạn gì thêm.

Sample Input

2
3 3
1 2
2 3
3 1
6 6
1 2
1 3
2 3
2 4
3 4
5 6

Sample Output

Khoa
Ngan

Note

Trong test ví dụ, ở ván đầu tiên thì Khoa chỉ cần xóa một điểm bất kỳ và lượt sau chắc chắn Ngân sẽ không thực hiện được nước đi hợp lệ.

Cụ thể hơn trong ván đầu tiên thì ván đấu có thể diễn ra như sau:

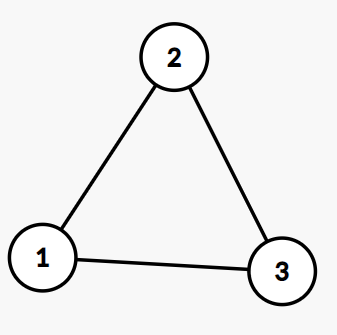
Khoa chọn điểm thứ ~2~ và xóa nó đi. Đồ thị trở thành như sau:

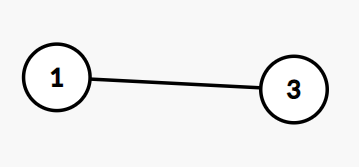
Do ~1~ và ~3~ đều chỉ có ~1~ đoạn thẳng nối tới nó (lẻ) nên Ngân sẽ không thể thực hiện lượt đi của mình và Khoa giành chiến thắng.