~\texttt{Rocks Papers Scissors}~ hay còn được gọi là kéo búa bao là một trò chơi đơn giản để phân định xem ai sẽ là người phải đi lấy đồ ăn được shipper giao, hay ai sẽ là người phải lau bảng...

gaogao là một người ghét sự đơn giản nên cô ấy đã phát minh ra một trò chơi gọi là ~\texttt{Rock Paper Scissors Lizard Spock}~.

Cụ thể, cách phân định thắng thua của trò chơi này được thể hiện qua ảnh sau:

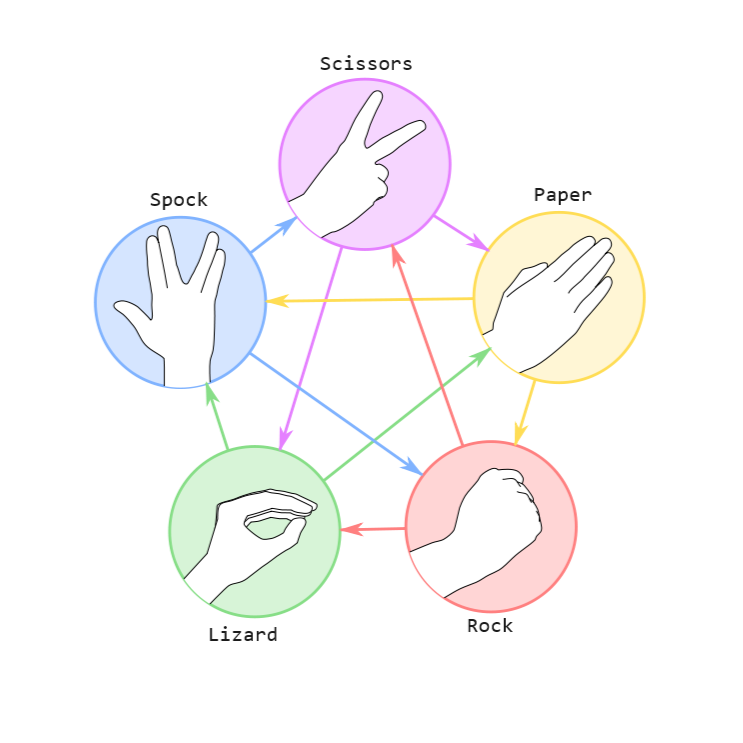
Ví dụ ta sẽ có như sau:

• Ô ~\texttt{Rock}~ màu đỏ có một mũi tên màu đỏ nối với ô ~\texttt{Lizard}~ nên ~\texttt{Rock}~ sẽ thắng ~\texttt{Lizard}~.
• Ô ~\texttt{Paper}~ màu vàng có một mũi tên màu vàng nối với ô ~\texttt{Spock}~ nên ~\texttt{Paper}~ sẽ thắng ~\texttt{Spock}~.

Bạn cần phải xác định ai sẽ thắng một ván chơi ~\texttt{Rock Paper Scissors Lizard Spock}~.

~\texttt{Input}~

• Gồm một dòng duy nhất chứa hai xâu ký tự thể hiện người chơi ra ~\texttt{Rock}~ hay ~\texttt{Paper}~ hay ~\texttt{Scissors}~ hay ~\texttt{Lizard}~ hay ~\texttt{Spock}~.

~\texttt{Output}~

• Gồm một dòng duy nhất chứa kết quả chơi, nếu như xảy ra kết quả hòa thì in ra màn hình từ ~\texttt{"Draw"}~ (không có dấu ngoặc kép).

~\texttt{Sample Input 1}~

Rock Lizard

~\texttt{Sample Output 1}~

Rock

~\texttt{Sample Input 2}~

Paper Scissors

~\texttt{Sample Output 2}~

Scissors

~\texttt{Sample Input 3}~

Spock Spock

~\texttt{Sample Ouput 3}~

Draw

~\texttt{Notes}~

Vạn vật dung hòa, ai cũng có điểm mạnh yếu, không có ai là hoàn hảo cả.

gaogao có một dãy số gồm ~n~ phần tử ~A=(a_1, a_2, a_3, \dots, a_{n-1}, a_{n})~. gaogao định nghĩa sức mạnh của dãy con liên tiếp từ ~l~ đến ~r~ được tính bằng công thức sau:

$$P(l, r) = \frac{\sum^{r}_{x=l}a_x}{r - l + 1} \times \left(\frac{1+\sqrt{5}}{2}\right)^{-1 \times (r - l)}$$

Nhắc lại, dãy con của một dãy được tạo ra bằng cách xóa đi một số phần tử ở đầu và một số phần tử ở cuối của dãy gốc (có thể không xóa).

Nhiệm vụ của bạn là tìm ra giá trị sức mạnh lớn nhất của một dãy con.

~\texttt{Input}~

• Dòng đầu tiên chứa một số nguyên ~n~ là số phần tử có trong dãy số của gaogao.
• Dòng thứ hai chứa ~n~ số nguyên là các phần tử có trong dãy số của gaogao.

~\texttt{Output}~

• Gồm một số thực duy nhất là giá trị sức mạnh lớn nhất của tất cả các dãy con.
• Bạn cần in ra chính xác số ~2~ chữ số thập phân.

~\texttt{Constraint}~

• ~1 \leq n \leq 10^6~.
• ~1 \leq a_i \leq 10^9~.

~\texttt{Subtask}~

• Subtask ~1~ (~50\%~ số điểm): ~n \leq 10^2~.
• Subtask ~2~ (~50\%~ số điểm): Giới hạn gốc.

~\texttt{Sample Input}~

3
1 2 3

~\texttt{Sample Output}~

3.00

~\texttt{Notes}~

• Chọn dãy con là dãy ~(3)~.

Trong thế kỷ ~\texttt{XXI}~ chúng ta thấy được sự phát triển vượt bậc của công nghệ trí tuệ nhân tạo (~\texttt{AI}~). Một trong những tính năng quan trọng nhất của một mô hình trí tuệ nhân tạo tốt là khả năng tự học, tức là ~\texttt{Machine Learning}~. Một mô hình được gọi là có khả năng tự học, khi và chỉ khi nó có thể tự cải thiện độ chính xác của mình mà không cần sự giám sát liên tục của con người.

Ở bài toán này bạn cần phải xây dựng một mô hình tự học đơn giản như sau: ban đầu bạn sẽ được cho tập ~S~ gồm ~n~ câu hỏi, sẽ có lần lượt ~Q~ thao tác, mỗi thao tác thuộc hai dạng như sau:

• ~\texttt{@ Q A}~: cung cấp thông tin rằng đáp án của câu hỏi thứ ~Q~ là xâu ~A~ (có thể có khoảng trắng).
• ~\texttt{? Q}~: hỏi với câu hỏi ~Q~ (là một chuỗi các ký tự có thể có khoảng trắng) thì đáp án là gì.

~\texttt{Input}~

• Dòng đầu tiên gồm số nguyên ~n~.
• ~n~ dòng tiếp theo, dòng thứ ~i~ chứa xâu thể hiện câu hỏi thứ ~i~
• Dòng tiếp theo gồm số nguyên ~q~
• ~q~ dòng cuối cùng, mỗi dòng biểu diễn một thao tác như trên.

~\texttt{Output}~

• Ứng với mỗi thao tác hỏi, in ra câu trả lời trên một dòng.

~\texttt{Sample Input}~

2
What is always approaching but never arrives?
The more you see the less there is?
5
@ 1 The future
? What is always approaching but never arrives?
? The more you see the less there is?
@ 2 Darkness
? The more you see the less there is?

~\texttt{Sample Output}~

The future
abcxyz
Darkness

~\texttt{Constraint}~

• ~1 \leq n, Q \leq 10^5~.

~\texttt{Subtask}~

• Subtask ~1~ (~50\%~ số điểm): câu trả lời luôn được cung cấp trước khi hỏi.
• Subtask ~2~ (~50\%~ số điểm): không có giới hạn gì thêm.

~\texttt{Scoring}~

Đối với mỗi test gọi ~J~ là số câu hỏi mà chương trình của BTC trả lời đúng còn ~P~ là số câu hỏi mà chương trình của bạn trả lời đúng điểm của bạn sẽ được tính như sau:

• Nếu ~P \ge J~ bạn đạt ~100\%~ số điểm test đó.
• Nếu ~P < 40\% \times J~ bạn đạt ~0\%~ số điểm test đó.
• Nếu ~40\% \times J \leq P \leq J~ bạn đạt ~\frac{P}{J}^5\times 100\%~ số điểm test đó.

"Đi date với con gái thì có nên đòi share bill không?" là câu hỏi được rất nhiều hảo hán mới hẹn hò lần đầu (hoặc nhiều lần) đặt ra!

Đối với LamTer thì anh không quan tâm việc có nên share bill không mà anh quan tâm tới việc share bill có chẵn hay không? LamTer cho rằng việc share bill sẽ chẵn khi giá tiền là một số "chẵn vcl" (chẵn vô cùng luôn). Một số được gọi là "chẵn vcl" khi và chỉ khi tất cả chữ số của nó là số chẵn. Ví dụ như số ~2024, 2222~ là số "chẵn vcl" trong khi ~2023, 1111~ không phải.

LamTer muốn biết đâu là số "chẵn vcl" lớn thứ ~n~.

~\texttt{Input}~

• Gồm một dòng duy nhất chứa số nguyên dương ~n~.

~\texttt{Output}~

• Gồm một dòng duy nhất chứa số "chẵn vcl" thứ ~n~.

~\texttt{Sample Input}~

133

~\texttt{Sample Output}~

2024

~\texttt{Constraint}~

• ~1 \leq n \leq 10^{12}~.

~\texttt{Notes}~

• Một vài số "chẵn vcl" đầu tiên là ~0, 2, 4, 6, 8, 20, 22, 24, 26, 28, 40, \dots...~.

Kì thi tốt nghiệp THPT năm 2024 đã trôi qua, báo hiệu sự kết thúc 12 năm học gian nan của lứa 2k6. heygnauq đã cùng bạn bè đi Đà Nẵng chơi một chuyến sau những ngày sống cùng sách vở.

Trong lúc tắm bồn ở khách sạn, heygnauq đã vô tình làm hư lỗ thoát nước mà không hề hay biết, cậu chỉ nhận ra lỗ thoát bị rò rỉ chỉ khi ngâm mình trong bồn tắm tĩnh lặng và đang nghĩ vu vơ về ai đó (hoặc về giáo án thầy Tu mù proxy cùng cô adc xúc tu). Bỗng chốc heygnauq nảy ra một ý tưởng, cậu thắc mắc liệu rằng có một bồn tắm có rất nhiều vòi nước và lỗ thoát nước cùng mở một lúc thì sau bao lâu, bồn tắm sẽ đầy hoặc cạn nước.

Vì quá bận đi chơi (~\texttt{LOL}~) nên heygnauq đành nhờ bạn giải quyết vấn đề đó.

~\texttt{Input}~

• Dòng đầu tiên chứa 2 số nguyên ~n, m~ lần lượt là số vòi nước và số lỗ thoát nước.
• ~n~ dòng tiếp theo, dòng thứ ~i~ là thời gian vòi thứ ~i~ chảy đầy bồn tắm không hở.
• ~m~ dòng tiếp theo, dòng thứ ~i~ là thời gian lỗ thứ ~i~ rút hết nước trong bồn khi bồn đầy nước.
• Dòng cuối cùng chứa một hữu tỉ ~t~ là lượng nước hiện tại trong bồn.
• Lưu ý:
  • Thời gian được cho dưới dạng giờ phút giây, ví dụ ~9~ giờ ~0~ phút ~24~ giây sẽ được biểu diễn là ~\texttt{9h0m24s}~. Cụ thể hơn ở test ví dụ.
  • Nếu số hữu tỉ đó vô hạn tuần hoàn thì sẽ được cho dưới dạng như sau: Ví dụ ~\texttt{0.8(83)}~ trong đó ~83~ chính là phần tuần hoàn.

~\texttt{Output}~

• Dòng đầu tiên in ra ~\texttt{FULL}~ hoặc ~\texttt{EMPTY}~ khi mực nước trong bồn đầy hoặc cạn sau một khoảng thời gian.
• Dòng tiếp theo in ra một chuỗi ký tự có dạng ~\texttt{P/Q}~ trong đó ~P/Q~ là số giờ để bồn đầy nước hoặc cạn nước dưới dạng phân số tối giản.

~\texttt{Sample Input}~

2 3
7h30m0s
5h0m0s
10h0m0s
15h37m30s
7h48m45s
0.05(63)

~\texttt{Sample Output}~

FULL
7785/341

~\texttt{Constraint}~

• Thời gian của các vòi nước và lỗ thoát luôn bé hơn ~1000~ giờ.
• ~1 \le n, m \le 100000~.
• ~0 < t < 1~.
• Dữ liệu đảm bảo ~P, Q < 10^{18}~.

~\texttt{Subtask}~

• Subtask ~1 \space (30\%)~: Thời gian của tất cả vòi và lỗ đều bằng nhau và đều có số phút, số giây bằng ~0~; ~t = 0.5~.
• Subtask ~2 \space (30\%)~: Thời gian của tất cả vòi bằng nhau, thời gian của tất cả lỗ bằng nhau.
• Subtask ~3 \space (40\%)~: Không có ràng buộc gì thêm.