Tin học trẻ Thừa Thiên Huế 2024 - Official Mirror
Điểm: 100
Tiến là một công nhân làm việc ở nhà máy socola QH. Công việc của anh là điều chỉnh nhiệt độ của hồ nhiệt độ. Hôm nay anh nhận được một đơn đặt hàng rất lớn đến từ Khoa. Vì là đơn đặt hàng rất lớn nên nhà máy đã đưa ra một quy trình để chuẩn hóa nhiệt độ như sau:
Cho hai dãy số nguyên độ dài ~N~ ~(N \leq 10^5)~:
- Dãy ~A~ gồm ~N~ số nguyên ~A = (a_1, a_2, a_3, \dots, a_N)~ ~(|a_i| \leq 10^9)~.
- Dãy ~T~ gồm ~N~ số nguyên ~T = (t_1, t_2, t_3, \dots, t_N)~ ~(1 \leq t_i \leq 3)~.
Quy trình chuẩn hóa sẽ gồm ~N~ bước, ở bước thứ ~i~ bạn cần phải:
- Với ~t_i = 1~ thì bạn cần tăng nhiệt độ của hồ nhiệt lên ~a_i~ đơn vị nhiệt độ.
- Với ~t_i = 2~, nếu nhiệt độ hồ nhiệt lớn hơn ~a_i~ thì bạn không làm gì cả, ngược lại thì thay đổi nhiệt độ hồ nhiệt thành ~a_i~.
- Với ~t_i = 3~, nếu nhiệt độ hồ nhiệt nhỏ hơn ~a_i~ thì bạn không làm gì cả, ngược lại thì thay đổi nhiệt độ hồ nhiệt thành ~a_i~.
Vì là đơn hàng rất lớn nên Tiến không thể để xảy ra bất kỳ sai sót nào. Tiến đã đặt ra ~Q~ ~(Q \leq 10^5)~ tình huống giả định, hỏi rằng nếu nhiệt độ ban đầu của hồ nhiệt là ~x_i~ ~(|x_i| \leq 10^9)~ thì sau ~N~ bước chuẩn hóa, nhiệt độ cuối cùng của hồ nhiệt sẽ là bao nhiêu?
Bạn hãy giúp Tiến thực hiện nhiệm vụ quan trọng này.
Input
- Dòng đầu tiên chứa số nguyên dương ~N~ là số bước trong quy trình chuẩn hóa.
- ~N~ dòng tiếp theo, dòng thứ ~i~ chứa cặp số nguyên ~a_i, t_i~.
- Dòng tiếp theo chứa số nguyên dương ~Q~ là số tình huống giả định mà bạn cần phải trả lời.
- Dòng tiếp theo chứa dãy số ~X = (x_1, x_2, x_3, \dots, x_Q)~ độ dài ~Q~ lần lượt là nhiệt độ ban đầu của hồ nhiệt trong các tình huống giả định.
Output
Bạn cần ghi ra ~Q~ dòng.
- Dòng thứ ~i~ chứa nhiệt độ của hồ nhiệt sau khi thực hiện xong ~N~ bước nếu nhiệt độ ban đầu là ~x_i~.
Subtask
- Subtask ~1~ (~10\%~ số điểm): ~Q = 1~.
- Subtask ~2~ (~10\%~ số điểm): ~N, Q \leq 5000~.
- Subtask ~3~ (~30\%~ số điểm): ~t_i \neq 1~.
- Subtask ~4~ (~50\%~ số điểm): không có giới hạn gì thêm.
Sample Input
3
-10 2
10 1
10 3
5
-15 -10 -5 0 5
Sample Output
0
0
5
10
10
Note
Ở tình huống giả định đầu tiên, nhiệt độ ban đầu là ~-15~ đơn vị nhiệt độ. Quy trình chuẩn hóa sẽ diễn ra như sau:
- Ở bước đầu tiên, ~t_1 = 2~ và ~a_1 = -10~, vì ~-15 < -10~ nên nhiệt độ của hồ nhiệt trở thành ~-10~.
- Ở bước thứ hai, ~t_2 = 1~ và ~a_2 = 10~, nhiệt độ của hồ nhiệt sẽ được tăng ~10~ đơn vị nhiệt độ và hồ nhiệt độ sẽ có nhiệt độ là ~0~.
- Ở bước cuối cùng, ~t_3=3~ và ~a_3=10~, vì ~0 < 10~ nên nhiệt độ của hồ nhiệt vẫn giữ nguyên là ~0~.
Sau khi hoàn thành quy trình chuẩn hóa thì nhiệt độ của hồ nhiệt là ~0~.
Điểm: 100
Khoa và Ngân là hai học sinh tài năng và đầy năng lượng. Hàng ngày, họ đọ tài trong mọi lĩnh vực, từ các bài kiểm tra đến các hoạt động ngoại khóa. Khoa luôn nỗ lực vượt qua Ngân, còn Ngân luôn tìm cách phản công và chống trả.
Một ngày nọ, họ quyết định tham gia một trò chơi mới - một trò chơi tưởng tượng, một trò chơi mà tất cả đều phải thể hiện sự sáng tạo và trí óc của mình.
Trò chơi sẽ bao gồm ~T~ ván, mỗi ván cả hai bạn sẽ được cho một hình gồm ~N~ điểm được đánh số từ ~1~ đến ~N~ và ~M~ đoạn nối giữa ~2~ điểm bất kỳ. Mỗi ván sẽ gồm nhiều lượt, bạn Khoa sẽ đi lượt đầu tiên, ở mỗi lượt thì người chơi của lượt đó cần phải chọn ra một điểm có số lượng đoạn thẳng nối với nó là chẵn và xóa đi điểm đó cùng các đoạn có một trong hai đầu mút là điểm đó. Đến lượt của ai mà người đó không thực hiện được hành động trên thì người đó sẽ thua.
Bạn hãy cho biết ở mỗi ván thì ai sẽ là người chiến thắng, biết rằng cả hai bạn đều là những người có lập luận logic, chiến thuật hoàn hảo và sẽ đưa ra cách chơi tối ưu nhất ở mọi tình huống.
Input
- Dòng đầu tiên chứa số nguyên dương ~T~ là số ván mà hai bạn sẽ chơi với nhau.
Trong mỗi ván:
- Dòng đầu tiên chứa hai số nguyên không âm ~N, M~ tương ứng là số lượng điểm và đoạn của hình.
- ~M~ dòng tiếp theo, dòng thứ ~i~ chứa hai số nguyên ~u, v~ (~1 \leq u, v \leq N~) thể hiện rằng đoạn thẳng thứ ~i~ nối giữa điểm thứ ~u~ và điểm thứ ~v~.
Output
- Gồm ~T~ dòng chứa kết quả của ~T~ ván đấu.
Với mỗi ván đấu:
- Nếu Khoa thắng thì bạn cần ghi ra “Khoa” (không có dấu ngoặc kép).
- Nếu Ngân thắng thì bạn cần ghi ra “Ngan” (không có dấu ngoặc kép).
Constraint
- ~1 \leq T \leq 10~.
- ~1 \leq N, M \leq 10^5~.
Subtask
- Subtask ~1~ (~15\%~ số điểm): ~N \leq 10~.
- Subtask ~2~ (~15\%~ số điểm): ~M = N - 1~ và từ một điểm bất kỳ có thể đi tới mọi điểm khác thông qua các đoạn thẳng.
- Subtask ~3~ (~15\%~ số điểm): Các điểm và đoạn thẳng không tạo thành chu trình.
- Subtask ~4~ (~55\%~ số điểm): không có giới hạn gì thêm.
Sample Input
2
3 3
1 2
2 3
3 1
6 6
1 2
1 3
2 3
2 4
3 4
5 6
Sample Output
Khoa
Ngan
Note
Trong test ví dụ, ở ván đầu tiên thì Khoa chỉ cần xóa một điểm bất kỳ và lượt sau chắc chắn Ngân sẽ không thực hiện được nước đi hợp lệ.
Cụ thể hơn trong ván đầu tiên thì ván đấu có thể diễn ra như sau:
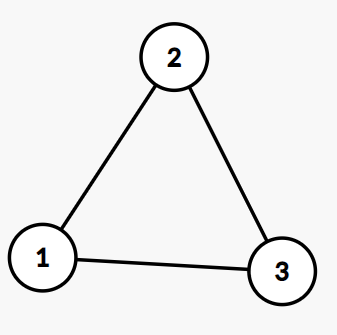
Khoa chọn điểm thứ ~2~ và xóa nó đi. Đồ thị trở thành như sau:
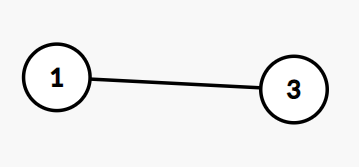
Do ~1~ và ~3~ đều chỉ có ~1~ đoạn thẳng nối tới nó (lẻ) nên Ngân sẽ không thể thực hiện lượt đi của mình và Khoa giành chiến thắng.
Điểm: 100
Quan niệm về may mắn và xui xẻo từ các con số đã trở thành một phần không thể thiếu trong cuộc sống, thể hiện qua những phong tục, truyền thống và các quy tắc ẩn. Với Khoa ~3, 6, 9~ được xem là những con số may mắn.
Trong ngày gặp lại Ngân – người bạn cũ của mình. Khoa muốn tặng cho Ngân ~k~ số nguyên không âm có tổng bằng với số may mắn của Ngân.
Khoa định nghĩa độ may mắn của ~k~ số chính là tổng độ may mắn của tất cả các chữ số trong ~k~ số đó. Độ may mắn của một chữ số phụ thuộc vào giá trị của chữ số đó và vị trí của nó. Cụ thể hơn, độ may mắn của một chữ số sẽ được thể hiện ở bảng sau:
| Chữ số | Hàng đơn vị | Hàng chục | Hàng trăm | Hàng nghìn | Hàng chục nghìn | Hàng trăm nghìn |
|---|---|---|---|---|---|---|
| ~3~ | ~F_0~ | ~F_1~ | ~F_2~ | ~F_3~ | ~F_4~ | ~F_5~ |
| ~6~ | ~2 \times F_0~ | ~2 \times F_1~ | ~2 \times F_2~ | ~2 \times F_3~ | ~2 \times F_4~ | ~2 \times F_5~ |
| ~9~ | ~3 \times F_0~ | ~3 \times F_1~ | ~3 \times F_2~ | ~3 \times F_3~ | ~3 \times F_4~ | ~3 \times F_5~ |
| Các chữ số khác | ~0~ | ~0~ | ~0~ | ~0~ | ~0~ | ~0~ |
Với ~F_0, F_1, F_2, F_3, F_4, F_5~ là các hằng số được cho trước. Ví dụ độ may mắn của số ~369~ là ~3 \times F_0 + 2 \times F_1 + F_2~.
Vì Khoa rất quý Ngân, nên Khoa muốn biết tổng độ may mắn tối đa của ~k~ số có tổng bằng số may mắn của Ngân. Tuy nhiên có một vấn đề là Khoa không hề biết số may mắn của Ngân là bao nhiêu? Nên anh đã đặt ra ~Q~ tình huống giả định.
Trong tình huống giả định thứ ~i~ hãy giả sử rằng ~x_i~ là số may mắn của Ngân, bạn cần cho biết độ may mắn tối đa của ~k~ số mà Khoa có thể tặng Ngân là bao nhiêu?
Input
- Dòng đầu tiên chứa số nguyên không âm ~k~ là số lượng số mà Khoa sẽ tặng Ngân.
- Dòng thứ hai chứa sáu số nguyên không âm ~F_0, F_1, F_2, F_3, F_4, F_5~.
- Dòng thứ ba chứa số nguyên không âm ~Q~ là số lượng tình huống giả định.
- ~Q~ dòng tiếp theo mỗi dòng chứa một số ~x_i~ tương ứng với số may mắn của Ngân trong giả định thứ ~i~.
Output
Gồm ~Q~ dòng:
- Dòng thứ ~i~ chứa độ may mắn lớn nhất của ~k~ số mà Khoa có thể tặng Ngân trong tình huống giả định thứ ~i~.
Constraint
- ~1 \leq k < 10^6~.
- ~1 \leq F_i \leq 10^9~.
- ~Q \le 10^6~
- ~1 \leq x_i < 10^6~
Subtask
- Subtask ~1~ (~5\%~ số điểm): ~x_i \leq 10~.
- Subtask ~2~ (~10\%~ số điểm): ~k \leq 100~ và ~Q = 1~.
- Subtask ~3~ (~30\%~ số điểm): ~Q = 1~.
- Subtask ~4~ (~40\%~ số điểm): ~k \leq 100~.
- Subtask ~5~ (~15\%~ số điểm): không có giới hạn gì thêm.
Sample Input
3
1 2 3 4 5 6
5
57
63
1313
2024
1805
Sample Output
11
8
27
38
33
Note
- Trong tình huống giả định đầu tiên Khoa sẽ tặng cho Ngân ~3~ số ~9, 9, 39~ (~9+9+39=57~).
- Thì khi đó độ may mắn sẽ là ~S = 3 \times F_0 + 3 \times F_0 + 3 \times F_0 + F_1 = 3 \times 1 + 3 \times 1 + 3 \times 1 + 3 \times 1 + 2 = 3 + 3 + 3 + 2 = 11.~
- Sẽ có những cách tặng khác, tuy nhiên thì cách tặng này là cách tặng có tổng độ may mắn lớn nhất.